Shortest Path Tree Problem

The Shortest Path Problem minimizes the weighted distance from one source node to one destination node. This module’s implementation is actually the Shortest Path Tree Problem, which solves the Shortest Path Problem for every possible destination node from a single source node.

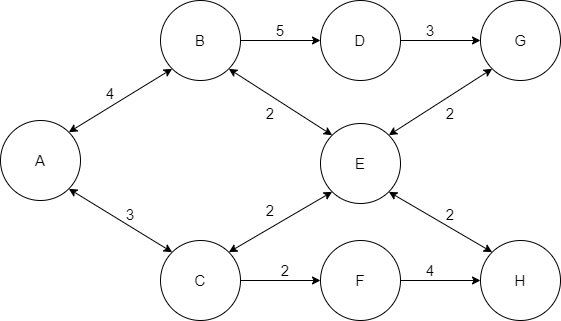
An example network is shown below. The arc lengths are shown as well, which can be interpreted as the cost of traveling an arc. Note that this graph is fully connected - there must be a possible path to every other node from the source node given.

Algorithm

Dijkstra’s algorithm finds an optimal solution to the shortest path tree problem as long as all of the weighted distances (costs of traveling an arc) are nonnegative. This explanation of the algorithm is from Jensen and Bard’s Operations Research Models and Methods (1, P. 195), with some differences in notation and explanation.

Initially, let the set \(\boldsymbol{S} = \{s\}\) and let \(\alpha_s = 0\).

Repeat until \(\boldsymbol{S}\) is the set of all nodes reachable by the source node:

Find an arc \(k(i, j)\) that passes from a solved node to an unsolved node such that:

\[k(i, j) = \text{argmin}\{\alpha_{i^{'}} + c_{k^{'}} : k^{'}(i^{'}, j^{'}) \in \boldsymbol{A}, i^{'} \in \boldsymbol{S}, j^{'} \in \boldsymbol{\bar{S}} \}\]

where \(\boldsymbol{\bar{S}}\) is the complement of the set \(boldsymbol{S}\). With the optimal arc \(k(i, j)\) from above, add node \(j\) and arc \(k(i, j)\) to the tree. Add node \(j\) to the solved set \(\boldsymbol{S}\). Let \(\alpha_j = \alpha_i + c_k\), where \(k \equiv k(i, j)\).

API Reference

See the corresponding section in the API Library Reference to learn more about how to use the API for this problem class.

1

Jensen, P. A., & Bard, J. F. (2002). Operations Research Models and Methods. Wiley.